Coloquio: El largo gracias
- 04-12-2025 14:00 |
- Aula Federman
* Por Gastón Giribet
En un artículo publicado el 21 de septiembre pasado, Cumrun Vafa, un reconocido experto en teoría de cuerdas y profesor de la Universidad de Harvard, propone, basándose en ciertos atributos de la teoría de cuerdas, lo que sería una nueva teoría acerca del universo temprano [1]. En los párrafos que siguen, reseño esta idea y el contexto en el que se da.
Pero, primero, comencemos poniendo las cosas en contexto: Desde hace algunos años, Vafa y algunos colaboradores propusieron y estudiaron lo que se conoce como “la conjetura del pantano” aplicada a la cosmología. Esta conjetura, grosso modo, establece la enorme dificultad, si no imposibilidad, de describir un universo tipo de Sitter en el marco de la teoría de cuerdas (recordemos que un “universo tipo de Sitter” es un universo cuya expansión es exponencial en el tiempo y, por lo tanto, es acelerada). De acuerdo con la conjetura del pantano, las soluciones a las ecuaciones de la teoría de cuerdas que parecen describir un universo tipo de Sitter no pertenecen al “paisaje” de soluciones verdaderas sino al temible “pantano” de soluciones aparentes que no son verdaderas soluciones [2,3].
A priori, esta dificultad teórica de describir un universo tipo de Sitter en el marco de la teoría de cuerdas podría parecer un problema. Esto se debe a dos razones: Por un lado, sabemos a partir de las observaciones cosmológicas (por ejemplo, las observaciones de supernovas distantes) que nuestro universo se encuentra hoy en expansión acelerada. Por otro lado, la mejor y más homologada teoría que tenemos para describir la etapa temprana del universo, la teoría de inflación, indica que también en esos primeros momentos el universo pasó por una fase de aceleración à la de Sitter. Ergo, aquí hay un conflicto doble, un problema cuya solución ha de estar dada por alguna de las tres explicaciones siguientes:
Así, la solución al conflicto entre la conjetura de Vafa y las observaciones cosmológicas puede ser a), puede ser b), puede ser c), o puede ser alguna combinación de algunas o todas ellas. Pero, como fuere, no es esto lo que nos convoca aquí, sino el paper de Vafa más reciente. Pasemos a nuestro asunto, pues:
El paper, decíamos, apareció este lunes en la base de datos de arXiv [1]. En él, Agrawal, Gukov, Obied y Vafa, basándose en una propiedad de la teoría de cuerdas llamada T-dualidad, sugieren que el universo temprano pudo haber tenido una “fase topológica”: ¿Fase topo-qué? Topológica. ¿Qué quiere decir eso? Bien … lo explico abajo, pero antes necesitamos un poco más de contexto:
Según la teoría de inflación, en las primeras fracciones de segundo después del Big-Bang el universo se infló exponencialmente compelido por la energía de un campo hipotético llamado “el inflatón”. En la versión más simple de la teoría inflacionaria, durante un lapso breve el campo inflatón cesa su fluctuar y guarda toda su energía en forma de energía potencial, lo que produce la densidad de energía (enorme) y la presión (igualmente enorme pero negativa) necesarias para disparar y sostener, aunque brevemente, la fase de aceleración cósmica. Luego de un período violento de inflación, durante el cual el universo duplicó su tamaño 60 veces en una ínfima fracción de segundo, la aceleración cesa, el universo se recalienta y, a partir de eso, nace la radiación y la materia que hoy conocemos.
Vafa et al., convencidos de que tal historia es imposible (o al menos está desfavorecida como hipótesis) en el marco de la teoría de cuerdas, consideran en [1] que es algo diferente lo que pudo haber ocurrido en ese universo primigenio. Proponen un escenario ciertamente distinto:
La teoría de cuerdas es una teoría con una arquitectura matemática rica y hermosa. Entre las más atractivas de sus propiedades se encuentran las llamadas “simetrías de dualidad”, que están, a su vez, detrás del atributo más interesante de la teoría: i.e. la teoría de cuerdas es “única”; a lo sumo, hay diferentes escorzos desde dónde mirarla.
Entre las varias simetrías de dualidad de la teoría de cuerdas, hay una que se destaca por la belleza de su descripción geométrica: La dualidad-T. Debido a la dualidad-T, existen muchas maneras, en apariencia distintas pero matemáticamente equivalentes, de describir las configuraciones de la teoría. Para darnos una idea, doy tres ejemplos: Según la T-dualidad:
1) Una configuración de la teoría de cuerdas en la que los entes fundamentales (las cuerdas) se mueven en un espacio-tiempo en el que sólo existe la gravedad, puede a veces ser pensada de manera equivalente como otra configuración, en apariencia distinta, en la que sólo hay campos como el magnético, pero no gravedad.
2) Una configuración en la que las dimensiones extra son pequeñas (recordemos que según la teoría de cuerdas el espacio no tiene sólo 3 dimensiones espaciales sino 9 de ellas, siendo que las 6 dimensiones “extra” nos son inaccesibles debido a su ínfimo tamaño) puede demostrarse equivalente a otra configuración en la que esas dimensiones extra son, por el contrario, enormes.
3) Una configuración en la que la energía se debe a que las cuerdas se enroscan varias vueltas sobre ellas mismas, tensionándose, puede demostrarse equivalente a otra configuración en la que no hay enroscamiento sino sólo quanta de impulso en las dimensiones extra.
Así, hay muchas (acaso infinitas) formas de ver una dada configuración física. De aquí, que todas las teorías de cuerdas que creíamos tener a comienzos de la década de los 90s resultaron, con el descubrimiento de las dualidades, ser la misma teoría: una única teoría de todo.
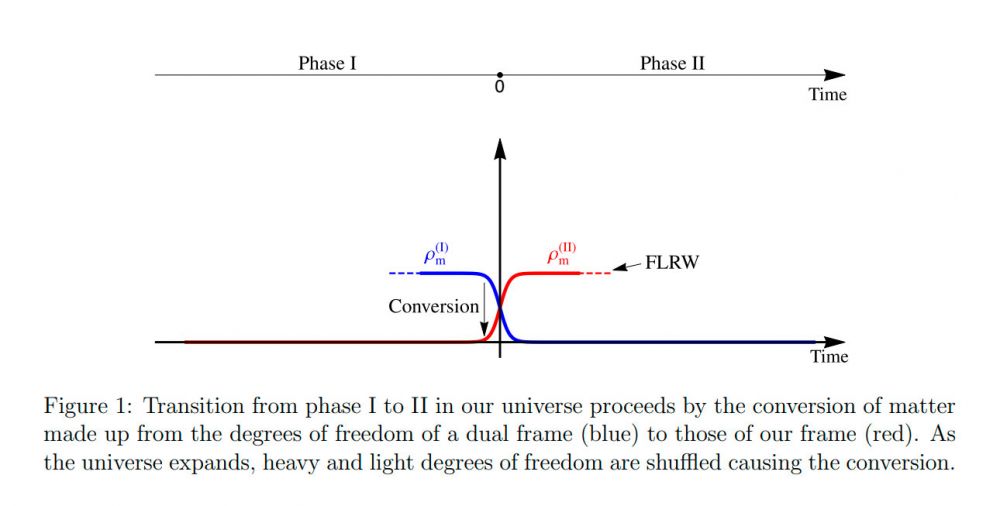
Otra lección que uno aprende de la teoría de cuerdas es que la descripción de la naturaleza en términos de la teoría cuántica de campos es sólo válida en cierto límite, en ciertos regímenes, pero de ningún modo válida en general. La teoría de campos sólo tiene sentido como “descripción efectiva”, como una aproximación válida a ciertas escalas, confiable hasta ciertos valores de energía. Así, puede ocurrir (y típicamente ocurre) que uno necesite más de una descripción efectiva de campos para describir la entera historia del cosmos, por ejemplo. Sería piadoso esperar que la teoría de campos que empleamos para describir nuestro universo hoy fuera válida también para describir el universo temprano, en el que la realidad era tan otra: tan densa, caliente, curvada. Ahora bien, debido a la dualidad-T, la teoría de cuerdas nos permite conectar las distintas descripciones efectivas de las diferentes etapas del universo: El truco es usar las reglas de la dualidad-T como diccionario. De esta manera, puede ocurrir que la etapa inicial del universo requiera, para ser explicada, una teoría distinta (pero traducible) a la que empleamos para describir nuestra física de partículas en el universo actual o en el futuro. Esta es una vieja idea, que se remonta a los trabajos de los 80s de Brandenberger y el mismo Vafa sobre la llamada “cosmología del gas de cuerdas” [4]; es una idea que está presente, también, en los trabajos de otros físicos, como Veneziano, quien hace décadas pensaba ya en “una cosmología de cuerdas pre-Big Bang”. De acuerdo a las versiones modernas de esta idea, como la reciente de Vafa, el universo habría tenido una etapa anterior a las que conocemos, una etapa en la que la materia (i.e. el contenido de campos) era muy distinta a la que conocemos hoy. Luego, habría habido una transición de fase al universo en su forma actual.
¿Qué ocurrió en esa transición de fase? ¿Qué podemos esperar de ese “empalme” entre dos fases tan diferentes del universo? ¿Cómo sería, mirándola hoy, desde lejos y desde el futuro, esa transición? Estas son preguntas que Vafa et al. encaran en su trabajo reciente, aunque aún falta elaborar sobre ellas.
La afirmación más importante del artículo de Vafa et al. es la siguiente: Debido al congelamiento de ciertos grados de libertad al pasar de una fase del universo a otra (i.e. de una descripción efectiva a otra) es posible modelar esa transición de fase como si en ese momento el universo estuviera gobernado por una teoría topológica. Ahora sí, expliquemos qué es esto:
Una teoría topológica es una teoría de campos que no contiene grados de libertad dinámicos, una teoría cuyo lagrangiano no depende de la métrica del espacio-tiempo, sino que forma una acción que es (o está íntimamente relacionada con) un invariante topológico, lo que los matemáticos llaman una clase característica. Para una teoría topológica de la gravedad, por ejemplo lo relevante es la topología del espacio-tiempo, no sus sutiles deformaciones o su oleaje o su fluctuar, a lo que una teoría tal sería insensible, sino los cambios abruptos de forma.
Ese momento de transición de fase acaecido en el universo temprano sería bien modelado, argumentan Vafa et al., por una teoría topológica. Más interesante aún es el hecho de que esto podría explicar varios aspectos observacionales de nuestro universo hoy: su planitud espacial, entre otros. A diferencia de (la mayoría de) las teorías de inflación, la fase topológica llevaría aparejados dos fenómenos: uno, la presencia de efectos de no-gaussianidad en las funciones de correlación de varios puntos; el otro, la ausencia de modos tensoriales en las fluctuaciones de la radiación cósmica de fondo.
Sin una certeza acerca de “cuál” sería precisamente la teoría topológica que describiría esa fase, en algún sentido rígida, del universo temprano, en su trabajo Vafa et al. consideran un ejemplo ilustrativo: la teoría de gravedad topológica de Witten, una linda construcción matemática de fines de los años 80s [5]. Es ésta una primera exploración de la idea, una idea que muchos tomaremos con cierto escepticismo, pero que, sin lugar a duda, es novedosa y merece ser investigada: Einstein nos convenció hace más de un siglo de que nuestro universo es geometría; ahora cabe preguntarse: ¿Fue en algún momento nuestro mundo simplemente topología?
Referencias
[1] P. Agrawal, S. Gukov, G. Obied y C. Vafa, arXiv:2009.10077. Link: https://arxiv.org/pdf/2009.10077.pdf
[2] H. Ooguri y C. Vafa, Nucl. Phys. B 766 (2007) p. 21.
[3] G. Obied, H. Ooguri, L. Spodyneiko y C. Vafa, arXiv:1806.08362.
[4] R. H. Brandenberger y C. Vafa, Phys. Rev. Lett. 60 (1988) p. 1229.
[5] E. Witten, Phys. Lett. B 206 (1988) p. 601.